The Concept of a Function
A quick review of useful functions and definitions introduced throughout precalculus, that will make many appearances during our course.
What is a Function?
A function is a precise, unambiguous rule for assigning each element of one set (called the domain) to a unique element of another set (called the range). Schematically, you’ll often see a function represented like this, to emphasize the three important parts of its definition:
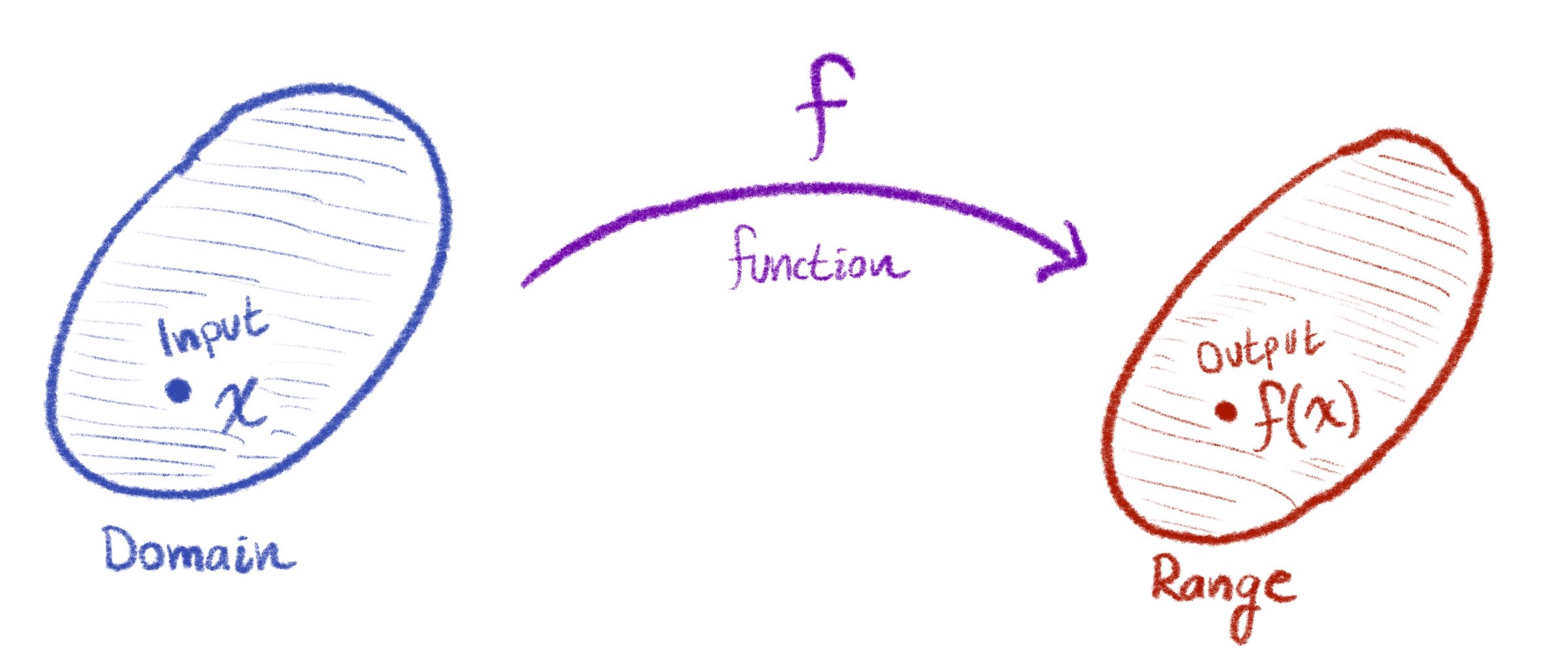
A function may be given by any such rule, between any two sets (for example, the rule which assigns each human being on earth to the date and time of their birth is a function!) but we will concentrate our interests primarily on functions for which both the domain and the range are subsets of the real number line. These ‘real valued’ functions are important across the STEM disciplines as a means of quantifying phenomena, and also comprise the rich mathematical playground in which calculus was first discovered.
The graph of a function is the set of
ordered pairs
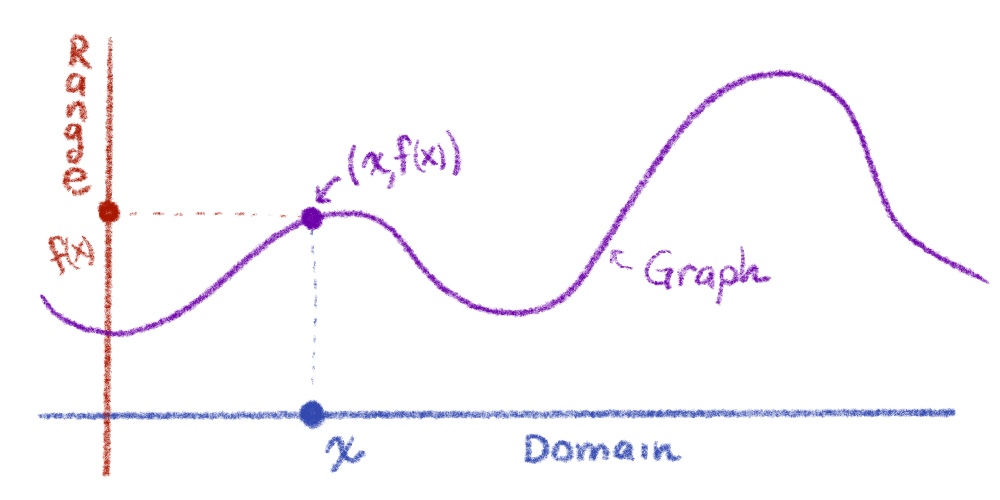
Drawing graphs is a great way to get a qualitative understanding of the behavior of a function. Things like what the function is doing (is it increasing in value, or decreasing?) does it reach a maximum value and then ‘turn around’? Etc. Indeed - we will discover much of calculus while trying to quantify some of these very notions!
1-to-1 and Onto
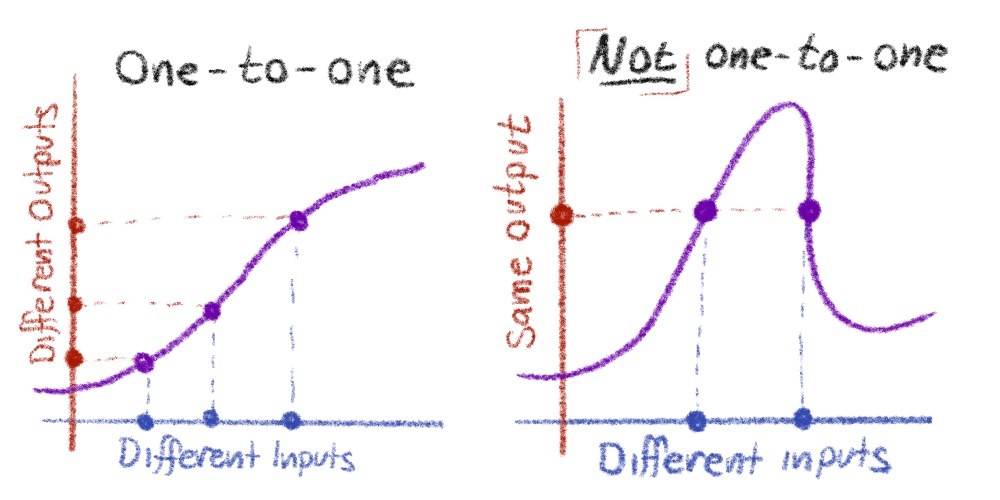
For every function, the output is unique for a given input, but it is absolutely allowable that many different inputs may give the same output (returning to the birthday example, any single person cannot have two different birthdays, but its relatively common for two distinct people to share the same birthdate!). When each output does come from a unique input, we call the function one-to-one (meaning every one input goes to one output, with no overlaps).
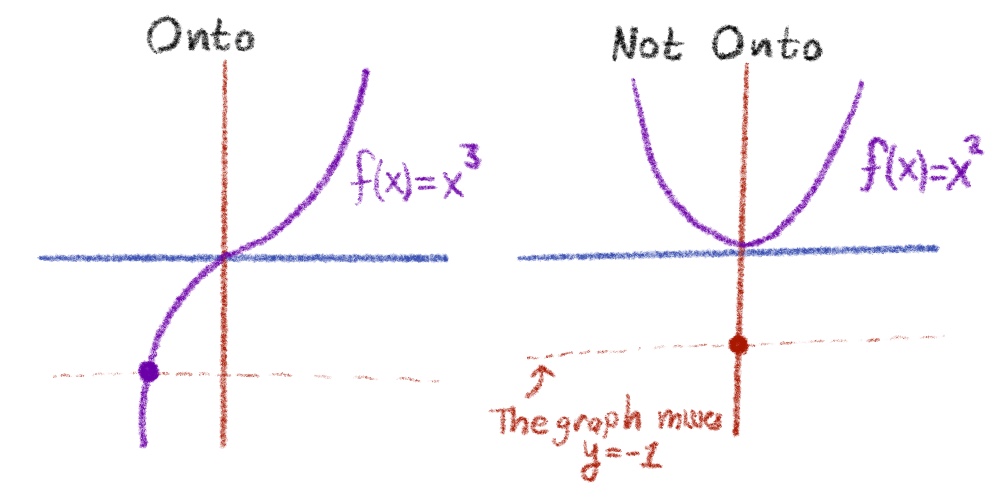
A function is also not required to have every single element of the range actually ‘hit’ by the output of some element of the domain. When this does happen, the function is called onto.
Function Composition
Some of the real power of working with functions comes from the ease of being able to create complex combinations, describing widely varying phenomena, out of very simple pieces. The most important tool in doing so is composition, or creating a new function by stringing two existing functions together. Pictorally, a composition looks like this:
PICTURE
The composition of
Inverse Functions
If a function is a rule for translating points of one set into another, the inverse function is a way of undoing this, and returning the outputs to the inputs they came from.
PICTURE
If
A function is called invertible if it has an inverse. Note that not every function is invertible!
As a classic example, consider the function