The Fundamental Theorem of Calculus
Differentiating the Area Function
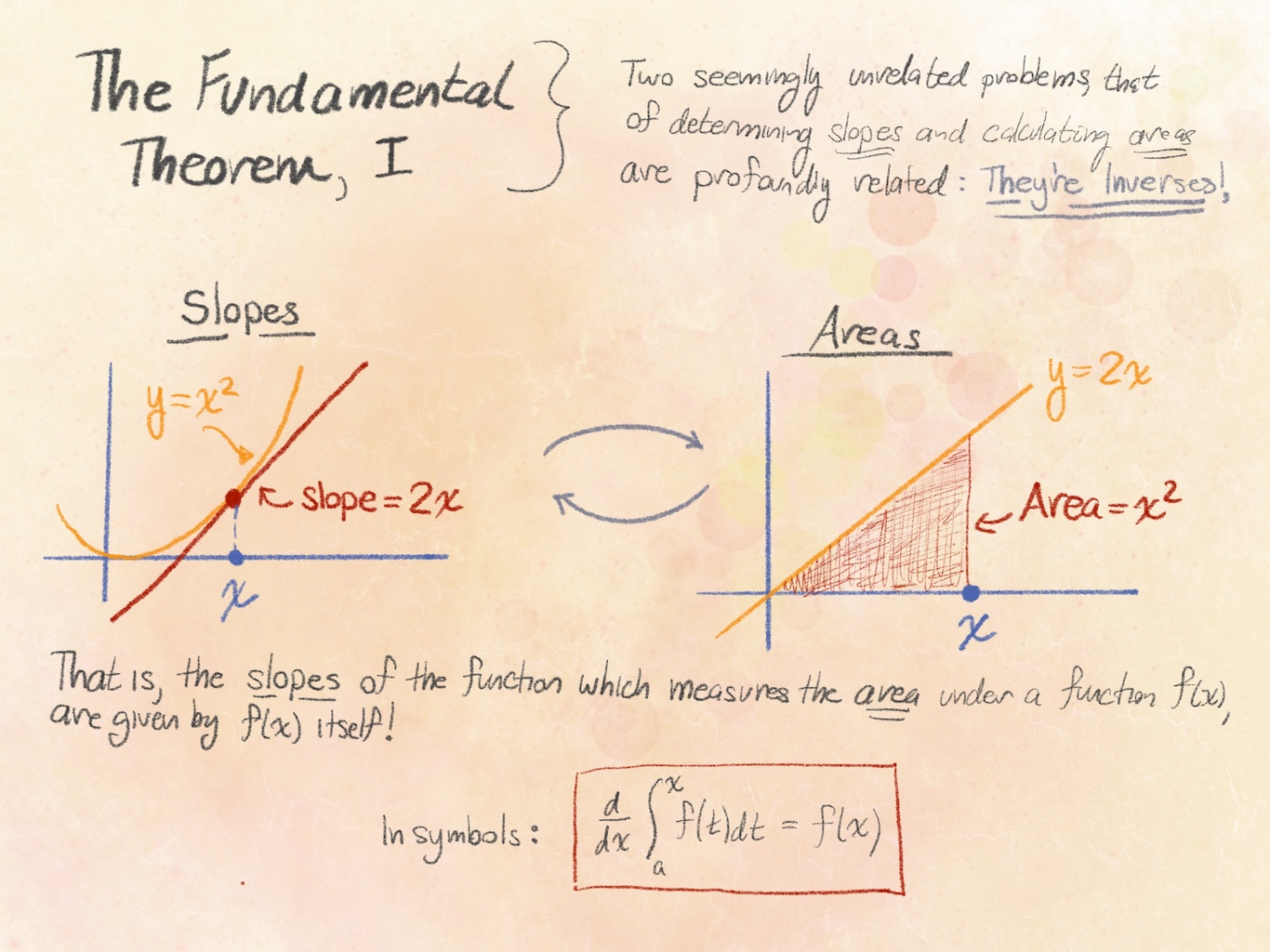
The fundamental theorem of calculus relates the problem of computing areas to the problem of finding slopes in a very
surprising way: it may be paraphrased as saying these two operations are inverses of one another. More precisely, if $f$
is a function and $\mathrm{Area}(x)$ measures the area under $f$ from some fixed starting point (say, $x=0$) to $x$,
then $\mathrm{Area}^\prime(x)=f(x)$.
(We will usually denote the area function by its familiar name: the definite integral $F(x)=\int_0^x f(t)dt$)
Here’s an interactive example, plotting in Desmos a function $f$, the definite integral $F=\int_0^x fdt$, and the derivative $F^\prime$ of $F$: you can see directly that $F^\prime = f$, as the fundamental theorem claims! (Feel free to change the function $f$ as you please)
Areas and Antiderivatives
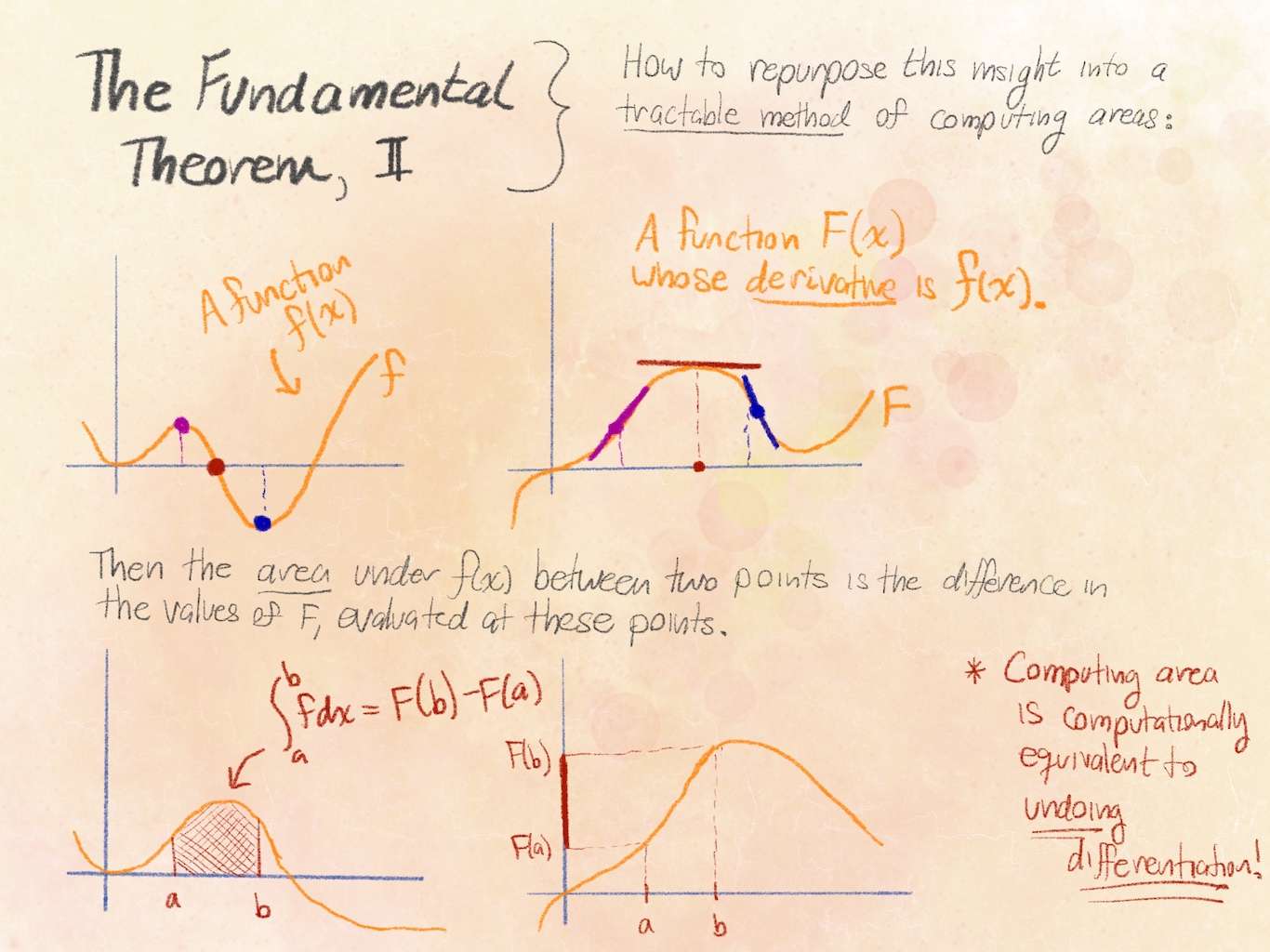
This gives us a practical means of computing areas: we can find the area function $\mathrm{Area}$ for any given function $f$ by simply tracking down functions which have $f$ as their derivative. Such functions are helpfully called antiderivatives, and the standard notation is to denote antiderivatives of a function (written by some lowercase letter, like $f$) by the capital of the same letter (so here, $F$). For example, if $f(x)=2x+1$ we may write $F(x)=x^2+x$ since $F^\prime(x)=f(x)$. These antiderivatives give us a simple means of computing areas:
The Indefinite Integral
One enduring complication is that antiderivatives are not unique: if $F$ is any function with $F^\prime=f$, then $F+2$, and $F+\pi$, and $F-13,053$ are also antiderivatives of $F$, since the derivative of any constant is zero! For some problems (such as the determination of areas), the particular antiderivative one chooses to work with is immaterial, and any one choice is as good as any other. But for other applications (such as solving differential equations) selecting the ‘correct’ antiderivative out of the entire set of possible antiderivatives of $f$ is crucially important, so we will do best to keep this distinction in mind from the very beginning.
To do so, we will supplement our notation for specific antiderivatives (which, recall, is just to use a capital version of the same letter denoting the original function being anti-differentiated) with a notation for the set of all possible antiderivatives. Because of their utility in integration, we call this latter collection the indefinite integral, and denote it as $\int fdx$. That is, while $\int_a^b fdx$ denotes a number, and $f(x), F(x)$ both denote functions, $\int f dx$ denotes a set of infinitely many functions
$$\int 2x+1 dx = { x^2+x, x^2+x+1, x^2+x+\pi, x^2+x+\frac{3\sqrt{5}}{17},\cdots }$$
This notation is rather unwieldly, so instead we adopt a shorthand: we denote by the symbol $g+C$ the set of all functions which differ from $g$ by the addition of some constant. That is, $x+C = x, x+1, x+3, x-14, \cdots$. This allows us to write $$\int f dx = F(x)+C$$ where $F$ is any particular antiderivative of $f$.